clc # command window 지우기
whos # 작업 공간의 변수들 확인하기
clear 변수명 # 해당 변수를 지울때 사용 , 실행 후 workspace에 없음
(% 와 #) # 한줄 주석배열의 정의
, 또는 ' ' 공백을 이용하여 열을 구분함
; 을 통해서 행을 구분함
>> A = [1 2 3]
A =
1 2 3
>> B = [4; 5; 6]
B =
4
5
6
>> C = [1 2 3; 4 5 6]
C =
1 2 3
4 5 6size() 함수
size() 함수를 활용하여 각 배열의 행과 열의 크기를 알 수 있음
>> size(A)
ans =
1 3
>> size(B)
ans =
3 1
>> size(C)
ans =
2 3
zeros(), ones()
배열의 요소를 모두 zeros()의 경우 0, ones()의 경우 1을 갖는 방법.
zeros(row, col)
>> zeros(3,3)
ans =
0 0 0
0 0 0
0 0 0
>> ones(2,1)
ans =
1
1
배열의 연산
: (콜론)
: 연산자를 활용하여 연속된 값의 생성과 인덱싱에 사용되는 범위 지정을 할 수 있음
시작값:증가값:끝 (이상: : 이하) (증가값이 1일 경우 생략 가능)
배열의 정의
>> a = [-1:0.1:1]
a =
Columns 1 through 5:
-1.0000 -0.9000 -0.8000 -0.7000 -0.6000
Columns 6 through 10:
-0.5000 -0.4000 -0.3000 -0.2000 -0.1000
Columns 11 through 15:
0 0.1000 0.2000 0.3000 0.4000
Columns 16 through 20:
0.5000 0.6000 0.7000 0.8000 0.9000
Column 21:
1.0000>> a = [1:2:6 -1 0]
a =
1 3 5 -1 0
인덱싱
인덱스를 셀때 다른 언어와 달리 첫번째 요소의 인덱스는 1부터 시작한다
>> a = [1:2:6 -1 0]
a =
1 3 5 -1 0
>> a(1)
ans = 1
>> a(3:5)
ans =
5 -1 0
+ (더하기), - (빼기)
배열과 스칼라의 연산
배열에 스칼라를 더하거나 빼면 배열의 모든 요소에 연산이 적용됨
>> a = [1 2 3; 4 5 6]
a =
1 2 3
4 5 6
>> a + 2
ans =
3 4 5
6 7 8
>> a - 2
ans =
-1 0 1
2 3 4
배열과 배열의 연산
같은 크기의 배열끼리 요소별 연산 수행
배열끼리 더하거나 빼려면 두 배열의 크기(차원)가 같아야 함. 다를 경우 오류
>> a = [1:2:6 -1 0]
a =
1 3 5 -1 0
>> b = [1 2 3 4 5]
b =
1 2 3 4 5
>> a + b
ans =
2 5 8 3 5
>> a - b
ans =
0 1 2 -5 -5*(곱셈), / (나눗셈)
배열과 스칼라 연산
배열에 스칼라를 곱하거나 나누면 배열의 모든 요소에 연산이 적용됨
>> a = [1 2 3; 4 5 6]
a =
1 2 3
4 5 6
>> a * 2
ans =
2 4 6
8 10 12
>> a / 2
ans =
0.5000 1.0000 1.5000
2.0000 2.5000 3.0000
배열과 배열 연산
1) 요소별 연산 ( .* , ./, .\)
같은 크기의 배열끼리 각 요소별 연산을 수행. ./ 와 .\은 동일함
(문장 끝의 ; 차이: ;이 있으면 출력 생략, 없으면 출력)
>> a = [1 2 3; 4 5 6];
>> b = [10 20 30; 40 50 60];
>> a .* b
ans =
10 40 90
160 250 360
>> a ./ b
ans =
0.1000 0.1000 0.1000
0.1000 0.1000 0.1000
2) 행렬 연산
(1) * 곱셈 (A * B)
A의 열 개수와 B의 행 개수가 같아야함 (A의 행 개수와 B의 열 개수가 같은 경우 X)
만약 A가 (m × n) 행렬이고, B가 (p × q) 행렬이라면,
A * B가 정의되려면 반드시 A의 열 개수 n과 B의 행 개수 p가 같아야 함
- A (m × n) * B (p × q)
- 행렬 곱셈 가능 조건: n = p (A의 열 개수 = B의 행 개수)
- 결과 행렬의 크기: (m × q)
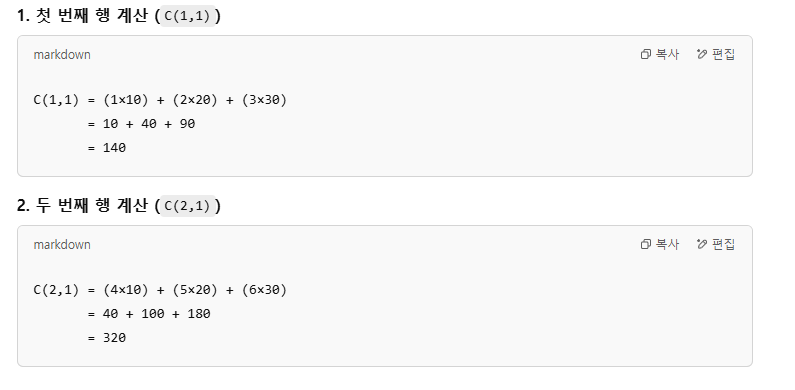
>> A = [1 2 3; 4 5 6]; # (2X3)
>> B = [10; 20; 30]; # (3X1)
>> C = A * B
C = #(2X1)
140
320
(2) / 나눗셈 ( A / B | A \ B)
오른쪽 나눗셈
A / B = A * inv(B) 즉, A * B의 역행렬임
그렇다면 행렬 곱셈과 마찬가지로 A의 열과 B의 행의 크기가 같아야 하며, 연산 후 결과값의 행의 크기는 A와, 열의 크기는 B와 동일해야한다. 이때, 역행렬은 늘 행과 열의 크기가 같으므로
A (m x n) / B (n x n) = C(m, n) 이 된다
왼쪽 나눗셈
A \ B = inv(A) * B 즉, A의 역행렬 * B 이다.
그렇다면 위와 마찬가지로 행렬 조건과 역행렬의 조건을 고려한다면
A (n, n) \ B(n,p) = C(n,p) 이 된다.
역행렬


^(제곱)
스칼라 제곱 ( .^)
곱셈과 나눗셈은 스칼라와 연산할때 .이 필요 없지만 제곱 연산자는 있어야함
>> t = 0:0.1:10;
>> y = t ^ 2;
error: for x^y, only square matrix arguments are permitted and one argu
ment must be scalar. Use .^ for elementwise power.
>> y = t .^ 2;
선형 그래프
plot() 선 그래프
plot(x값, y값)
xlabel() , ylabel() 각각 x축과 y축의 label 추가
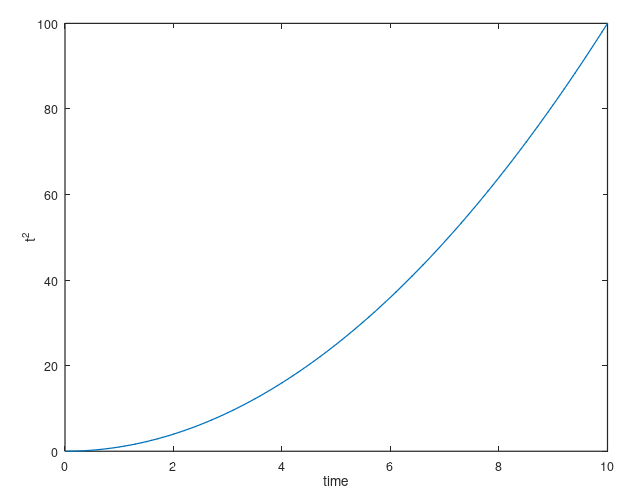
>> t = 0:0.1:10;
>> y = t .* t;
>> plot(t, y)
>> xlabel("time")
>> ylabel("t^2")
반복문
for i = 최소값:증감값:최대값
명령어
endfor
>> for i = 1:3:5
i
endfor
i = 1
i = 4
>> v = [1,2,3,4,5]
v =
1 2 3 4 5
>> for i = 1:1:5
v(i) = i
endfor
v =
1 2 3 4 5
v =
1 2 3 4 5
v =
1 2 3 4 5
v =
1 2 3 4 5
v =
1 2 3 4 5
>> for i = 1:1:5
v(6-i) = i
endfor
v =
1 2 3 4 1
v =
1 2 3 2 1
v =
1 2 3 2 1
v =
1 4 3 2 1
v =
5 4 3 2 1
이중 for문
for i = 1:3
for j = 1:3
p(i,j) = 3 * (i-1) + j
endfor
endfor
p =
1 2 3
4 5 6
7 8 9
p =
1 2 3
4 5 6
7 8 9
p =
1 2 3
4 5 6
7 8 9
p =
1 2 3
4 5 6
7 8 9
p =
1 2 3
4 5 6
7 8 9
p =
1 2 3
4 5 6
7 8 9
p =
1 2 3
4 5 6
7 8 9
p =
1 2 3
4 5 6
7 8 9
p =
1 2 3
4 5 6
7 8 9
sin() 사인 함수
sin(90)의 결과가 1이 아닌 이유: 인자의 단위가 라디안이기 때문이다 따라서
해당 인자를 r(각도) * 90 / 180 으로 입력해야 원하는 각에 대한 값이 나온다.
>> sin(90)
ans = 0.8940
>> sin(90 * pi / 180)
ans = 1exp() 함수
exp(x) 은 e^x의 값이다
>> exp(1)
ans = 2.7183사용자 정의 함수
function 반환변수 = 함수이름(매개변수)
반환변수 = 함수 코드;
endfunction
% sum function
function returnValue = sum(a,b)
returnValue = a + b;
endfunction
>> sum(1,2)
ans = 3